Master Natural Logs Rules Easily: A Simplified Guide

Natural logs can look complicated, intimidating, and incredibly confusing. Still, this math topic is not as bad as it may seem at first glance. Log expressions obey their own rules. Once you master these natural log rules, you will win any complex logarithm. So, how do you figure out them all? 

For this purpose, we have prepared a guide on six rules of logarithms for mastering natural logs. Visual examples, tips, and math insights will be useful to you. You’ll have a better understanding of the topic and feel confident on the exam. So, what are you waiting for? Become an expert in logarithms with our blog.

What Is a Natural Log and Why Do You Need to Understand It?

What is a natural log, and why do you need it at all? In this section, we will review the properties and characteristics of logarithms.

Key Natural Log Features

The natural logarithm is labeled ‘ln’ (loge = ln), the inverse of ‘e.’ What does this letter mean? The ‘e’ is a mathematical constant or natural exponent. For example, just like the number ?, it has a particular value, which is approximately 2.71828. 

What are the main features of the natural log? To understand them, you need to consider several scenarios presented below. They describe how ln acts in different situations.

How can you find the natural logarithm? There are several ways. First, you can use a calculator with the ln function. Second, there are special tables (like the one below) with the correct value for each number. 

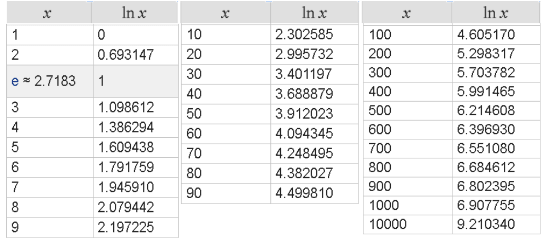
Source: RapidTables

Does Natural Log Differ From Other Logarithms?

Actually, the main difference between natural and common logarithms is the base. Common ones use 10 as a base, whereas the ln always uses e. Remember that logarithm rules are the same for both types. This means that ln(x)=loge(x).

Still, is it possible to turn one into the other? Yes. If you will ever need to convert ordinary logs to natural ones, you can use the following equations:

• log10(x) = ln(x) / ln(10)
• ln(x) = log10(x) / log10(e)

Why Do You Need to Understand Logarithms?

You are probably wondering why you need to know natural logarithms. First, you may face them in the SAT or ACT exam. The Math section of these tests may include tasks related to logarithmic function. Secondly, logs are often used in economics. Therefore, you should have at least a basic understanding of the topic.

6 Key Natural Log Rules With Examples

So, are you ready to master a natural logarithm once and for all? If yes, we have six logarithm  rules to help you do it effectively:

#1 Product Rule 

This rule states that the natural logarithm of x and y multiplication equals the sum of ln x and ln y. Let’s have some practice and look at some equations.

EXAMPLE: ln(4)(9) = ln(4) + ln(9)

• You should start with the left-hand side ln(4)(9). Apply the product rule, which says it equals the sum of In(x) and In(y).
• You can evaluate ln(4) and ln(9) separately. Remember that ln(4) is the natural logarithm of 4. Are there any ways to find it? Yes, try to perform a calculation using a calculator or a reference table, and you’ll get approximately 1.3863. Then, you can do the same operation with the ln(9), which will be about 2.1972.
• Next, substitute these values in the initial expression: ln(4)(9) = 1.3863 + 2.1972.
• Finally, the result of adding the two of them together is 3.5835.
• So, if you use the product rule for logs ln(4)(9), you’ll get 3.5835.

#2 Quotient Rule 

The quotient rule log says that the logarithm of dividing x and y is the difference between them. Let’s go into more detail about how this method works in practice. 

Example:  ln(18/5) = ln(18) – ln(5)

• So, apply the quotation rule stating that the first part equals ln(18) minus ln(5).
• Next, you should calculate each number separately. Thus, ln(18) is 2.8904, and ln(5) is 1.6094.
• After you substitute these values back into the log expression and subtract them, you will get the answer: ln(18/5) = 2.8904 – 1.6094 = 1.2810

#3 Power Rule

What do you know about the logarithm power rule? It’s pretty simple and states that the natural log of x raised to degree y equals y multiplied by ln x. 

• Suppose we have a logarithmic expression. Let it be the following: ln(7²) = 2 ? ln(7)
• Apply the power rule to the above equation. Now, evaluate ln(7), which is 1.9459.
• Substitute this value in the equation: 2  ? ln(7) = 2  ? 1.9459.
• Multiply the two values together and get the result of 3.8918.

This example demonstrates how to apply the power rule to find the natural logarithm of a number raised to an exponent.

#4 Reciprocal Rule

The natural log of the inverse of x is the opposite of ln of x. This idea is pretty straightforward, but sometimes, a negative number could bring some confusion.

Example: ln(1/5) = -ln(5)

• First, apply the reciprocal rule, where x equals 5 for this example.
• Then, calculate the ln of 5, which is about 1.6094. Do not forget to negate this value as per the reciprocal rule and get the answer: -ln(5) ? -1.6094.

#5 Derivative of Natural Logarithm

The derivative of the natural logarithm is the reciprocal of the inverse function. Let’s practice to get a better understanding.

Example: f(x) = ln(2x)

• To find the derivative denoted as f'(x), we can use f'(x) = 1 / x rule.
• Now, let’s compute the derivative of our expression: f'(x) = d/dx[ln(2x)].
• Next, find the derivative of 2x concerning x, which is 2: f'(x) = (1 / (2x)) ? 2.
• Finally, simplify the equation, and the derivative of our initial function is f'(x) = 1 / x.

#6 Integral of Natural Log

When you want to find the indefinite integral of ln(x), you can use the following formula:

Here, C represents the constant, which can take any real value. 

Example: f(x) = ln(2x).

• First, compute the integral of f(x) = ln(2x), which results in ? ln(2x) dx.
• Second, we need to apply a u-substitution to simplify the integral. Suppose u = 2x, which means du/dx = 2, or dx = (1/2)du.
• Now, it’s possible to rewrite the integral in terms of u and get ? ln(u) ? (1/2)du.
• Next, use the formula ? ln(u) ? (1/2)du = (1/2) ? ? ln(u) du.
• After, we can integrate ln(u) concerning u and get (1/2) ? ? ln(u) du = (1/2) ? (u ? (ln(u) – 1) + C).
• Here, u needs to be replaced with 2x: (1/2) ? (2x ? (ln(2x) – 1) + C).
• Finally, let’s simplify the expression: x ? (ln(2x) – 1) + C.
• So, the indefinite integral of the function f(x) = ln(2x) is? ln(2x) dx = x ? (ln(2x) – 1) + C.

How to Learn Complex Logarithms

Learning algorithms may seem challenging, but it’s much more straightforward. It all depends on how systematically you study. You have several options. For instance, you can learn independently using available resources like books and online services.

Source: Pexels

Perhaps you will have a lot of questions in the process. If necessary, seek help from a certified tutor. Usually, they provide helpful advice and tips on improving math skills. Besides, you can go through the topic in more detail or spend time on problematic areas. 

Another benefit of studying with a tutor is the individual approach. Usually, there are many students in regular school classes. Thus, the teacher does not have enough time to pay attention to each of them. Meanwhile, studying with a tutor, you get personalized attention.

Still, keep in mind that practice means a lot. Learning the log rules by heart and solving a few equations is not enough. Only regular studying and practicing could level up your knowledge. As a result, you will be confident in the final exam.

Conclusion

As you might realize, a logarithmic expression is not as complicated as it might look before. Practice and successfully solve complex tasks using the product, reciprocal, quotient rule log, and other tips that will help you master this topic well. Thus, you’ll perform well during your math finals.